The Lowest Common Ancestor or Least Common Ancestor (LCA) algorithm is a classic computer science problem, and one that I’ve had somewhat of a storied personal experience with over my years as a software engineer. Whether you are new to computer science, brushing up for an interview or just a curious individual, I hope you will enjoy this article!

Problem Overview

First things first, let’s start with a simple definition of the problem, don’t worry if it sounds a bit abstract at first, I promise it is not that bad.

Given a tree or directed acyclic graph and two nodes v & w, find the deepest node T, such that T is both a parent of v and w.

In more plain terms, given two family members, find the first common ancestor they both share. Given the tree in the image below, the LCA of nodes E & H would be node B, since node B.

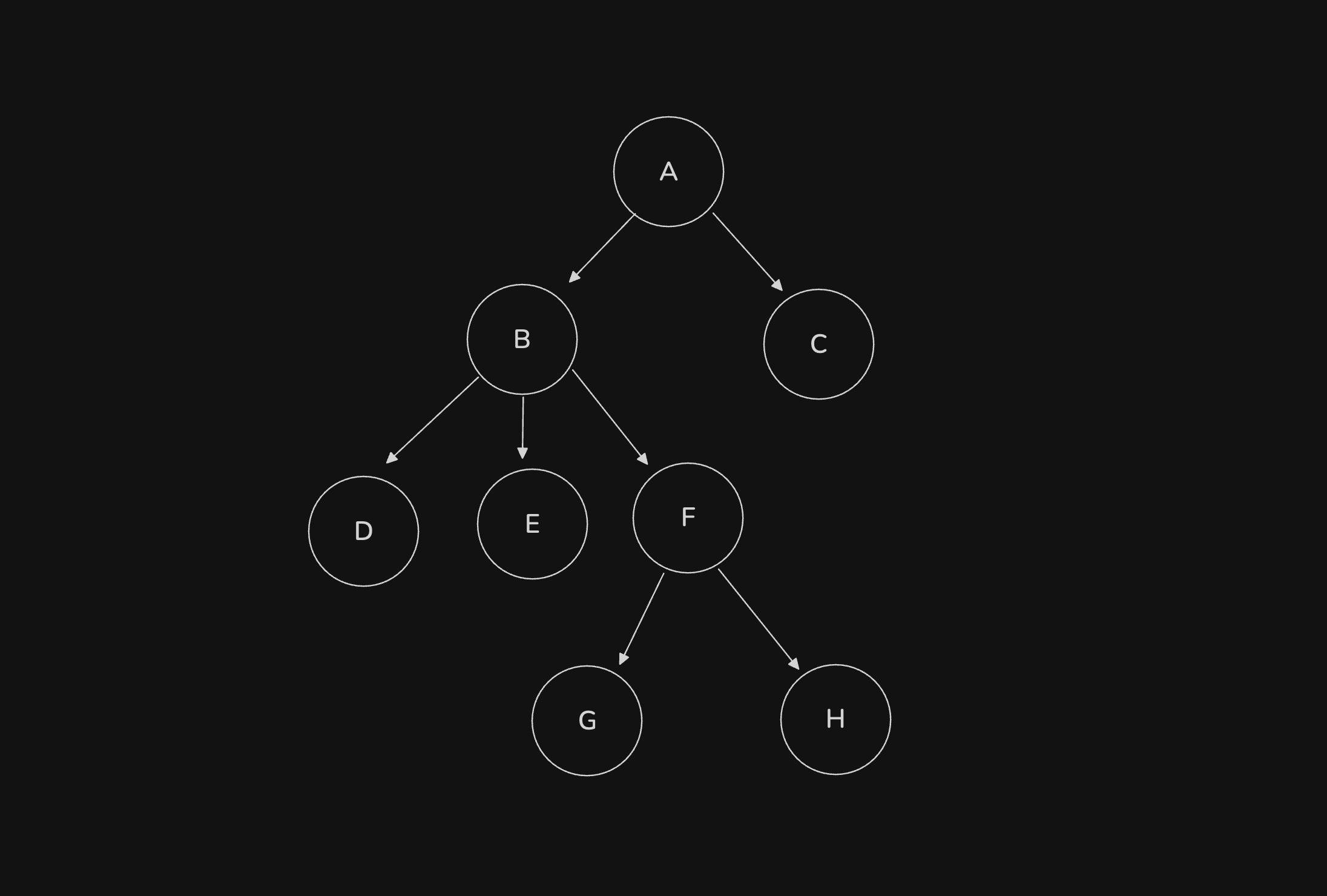
A couple things to note as well, each node can have an arbitrary number of children and can be arranged in any sort of particular order. Also a node is considered a direct descendent of itself, so the LCA of node F and H in this example would just be node F.

Implementing the Tree

Now that we have a basic understanding of the problem, let’s start writing some code! I will be using Typescript for the actual implementation, but it shouldn’t be too hard to follow if you are coming from another programming language as well.

First, let’s define the shape of our node which will be used to recreate the tree above, each node will contain a string value (A, B, C, etc.) and an array of children nodes. I will be writing the node as a class, but this could just as easily be a simple object as well.

class TreeNode {
  public value: string
  public children: TreeNode[] = []

  constructor(value: string) {
    this.value = value
  }
}

Next, let’s add some helper methods for common tree operations, which will be useful for building out our tree. We can start by adding a simple method for retrieving a specific node for a given value:

class TreeNode {
  // ...

  public find(value: string): TreeNode | undefined {
    if (this.value === value) return this

    for (const child of this.children) {
      const found = child.find(value)
      if (found) return found
    }

    return undefined
  }
}

The find(value: string) method will return if the current node if the provided value matches the nodes value, otherwise it will recursively check each child node until a match is found. If no match is found, then this method should just return undefined.

Next, let’s write another helper method which will find a node for a given value, and then insert a new child node. This will be quite useful for building the tree.

class TreeNode {
  // ...

  public insert(value: string, parentValue: string): TreeNode {
    const parent = this.find(parentValue)
    if (!parent) {
      throw new Error(`Failed to find node "${parentValue}"`)
    }
    const child = new TreeNode(value)
    parent.children.push(child)
    return child
  }
}

The insert(value: string, parentValue: string) method will attempt to find a node in the current tree with the parentValue, and if found, insert a new node with the given value as a child. If the parent node cannot be found, this method will throw an error.

Finally, let’s add one more method which will return the values of our tree as an in-order array of strings. To do this we will just create an array containing the current nodes value, then we will add all the values of each child’s subtree recursively.

class TreeNode {
  // ...

  public getSubtree(): string[] {
    const tree = [this.value]
    for (const child of this.children) {
      const subtree = child.getSubtree()
      for (const childValue of subtree) {
        tree.push(childValue)
      }
    }
    return tree
  }
}

Please note that I’ve written the getSubstree() method above in a way which should be understandable for people coming from different languages, but this does come with a slight performance penalty. For this example it shouldn’t matter too much, but as an exercise left for the reader, can you write this method such that we only need to instantiate an array once?

Ok, now that we have finished adding our helper methods, the full TreeNode class should look something like the following:

class TreeNode {
  public value: string
  public children: TreeNode[] = []

  constructor(value: string) {
    this.value = value
  }

  public find(value: string): TreeNode | undefined {
    if (this.value === value) return this
    for (const child of this.children) {
      const found = child.find(value)
      if (found) return found
    }
    return undefined
  }

  public insert(value: string, parentValue: string): TreeNode {
    const parent = this.find(parentValue)
    if (!parent) {
      throw new Error(`Failed to find node "${parentValue}"`)
    }
    const child = new TreeNode(value)
    parent.children.push(child)
    return child
  }

  public getSubtree(): string[] {
    const tree = [this.value]
    for (const child of this.children) {
      const subtree = child.getSubtree()
      for (const subTreeValue of subtree) {
        tree.push(subTreeValue)
      }
    }
    return tree
  }
}

Now let’s go ahead and instantiate our tree from the original example, all we need to do is create our root node and call our helper methods:

const root = new TreeNode('A')
root.insert('B', 'A')
root.insert('C', 'A')
root.insert('D', 'B')
root.insert('E', 'B')
root.insert('F', 'B')
root.insert('G', 'F')
root.insert('H', 'F')

We can verify that our tree has been built correctly by calling the getSubtree() on our root, which should return the following in-order array ["A", "B", "D", "E", "F", "G", "H", "C"].

const output = root.getSubtree()
console.log(output)

Click here to view on the Typescript Playground!

Designing the Algorithm

Now that we have a tree we can test, let’s start designing our Lowest Common Ancestor algorithm by first defining the shape of our function. In this example, we will write a function which takes the root node of a tree along with two values, and returns the least common ancestor they share.

function getLCA(root: TreeNode, value1: string, value2: string) {
  // ...
}

There are several ways to solve this, but we will start will a simple recursive approach. When approaching recursive problems, it is generally a good idea to start by defining our base case.

Since we are looking for a node which is both an ancestor of value1 and value2, our base case should just return the current nodes values when these conditions are satisfied. Now how should for this condition?

Remember our find(value: string) helper method above, we can use this check if a child exists at a current node, by checking if it returns a TreeNode or undefined.

function getLCA(root: TreeNode, value1: string, value2: string) {
  if (root.find(value1) && root.find(value2)) return root.value

  return undefined
}

Once we find a node that is a direct ancestor of both value1 and value2, all we need to do is return the current node all the way up the call stack, otherwise we should return undefined. Let’s test our base case with a simple example:

console.log(getLCA(root, 'B', 'C')) // outputs "A"

Awesome, we have now just implemented the logic to check if a node is an ancestor! While this does return an ancestor of two nodes, this is not guaranteed to be the least common ancestor.

To check for the least common ancestor, all we need to do is traverse the tree recursively until we find the last node for which our base condition evaluates to true.

Since the root node of a tree will always be an ancestor of any sub-values in the tree, we should add our traversal logic before our base case. We can do this by first checking if any of the child nodes are the LCA:

function getLCA(
  root: TreeNode,
  value1: string,
  value2: string
): string | undefined {
  // first check children subtree for LCA
  for (const child of root.children) {
    const found = getLCA(child, value1, value2)
    if (found) return found
  }

  // the check if current node is the LCA
  if (root.find(value1) && root.find(value2)) {
    return root.value
  }

  // if current node or subtree does not contain
  // the LCA then return undefined
  return undefined
}

Please note I also added a return type to the function, which is just string or undefined. Sweet, now let’s write some test cases and check if our solution works!

console.log(getLCA(root, 'B', 'C') === 'A')
console.log(getLCA(root, 'D', 'F') === 'B')
console.log(getLCA(root, 'D', 'G') === 'B')
console.log(getLCA(root, 'F', 'H') === 'F')
console.log(getLCA(root, 'F', 'Z') === undefined) // edge case

If you followed all of the steps above, each of these should output true to the console!

Click here to view full example!